선형대수학
선형: linearity(직선/ 비선형)
ex) 벡터, 행렬
vector: 크기와 방향이 있는 물리량 (스칼라의 묶음), 1차원 물리량
scaler: 크기가 있고 방향이 없는 물리량 -> R(상수), 0차원 물리량
scaler와 vector의 표현방법
N(자연수의 집합)
Z(정수의 집합)
Q(유리수의 집합)
R(실수의 집합)
{1,0,0,0} -> {1, 0]^4 : 0과 1 요소가 들어있고, 4개의 성분으로 되어있다.
ex) R^3 => {실수1, 실수2, 실수3}
0차원: 스칼라 scaler : R,
1차원: 벡터 vector: R^n
2차원: 행렬 matrix: R^(nxm)
( ■ ○ ■ ■ ) < row :n
( ■ ○ ■ ★ ) < row
( ■ ○ ■ ■ ) < row
^ ^ ^ ^ column : m
※행렬을 볼때는 row부터 본다 (2, 4)위치에 ★이 있다.
a = [1, 0, 2, 3, 4]
A = [3 0 1]
[2 0 3]
vector: a[3] = 2, a3 = 2
matrix: A[1,3] = 1, A1.3 = 1
3차원이상 tensor : Aijk(3차원), Aijkl(4차원)
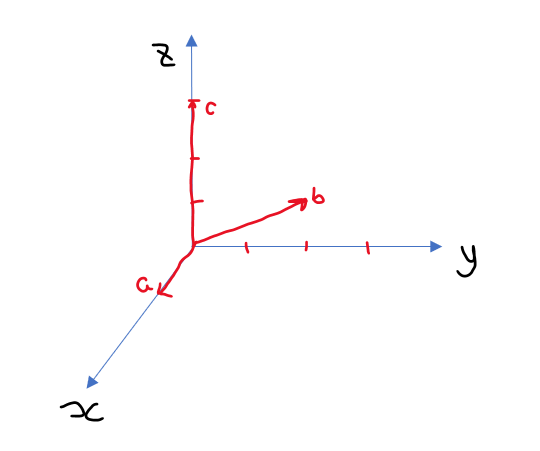
vector연산 // a ∈ R^n, b ∈ R^n
a+b 벡터의 사이즈가 다르다면 덧셈불가
axb 벡터의 사이즈가 다르다면 곱셈불가
-내적(inner product): a, b => a º b // 내적의 결과는 스칼라, 값은 |a||b|cosθ
-외적(outer product): a, b => a x b // 외적의 결과는 벡터
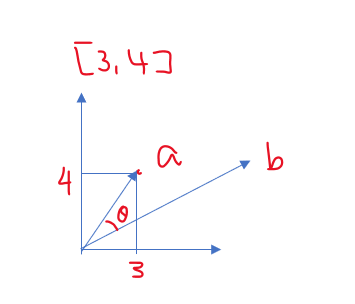
|a| = vector norm (크기)
|[3, 4]| = 5 = root(3^2 + 4^2)
θ : 두 vector사이의 사잇각
내적
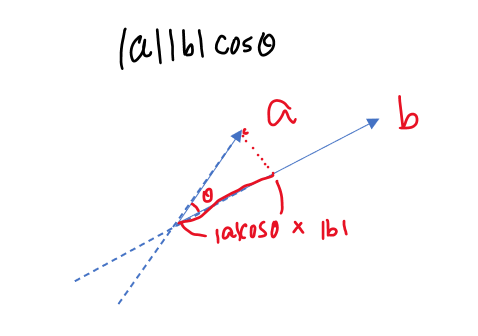
b세계에서 봤을때
a의 크기는 |a|cosθ
그것에 b의 크기를 곱한 것이 내적이다.
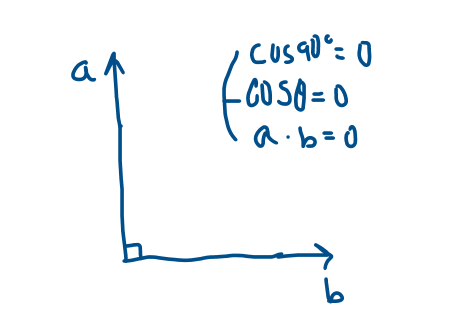
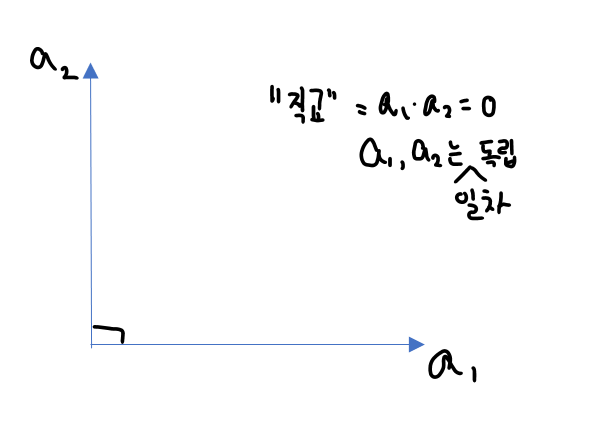
☆직교(orthogonal)
외적 (a ∈ R^n, b ∈ R^n)
a x b = c ∈ R^n
3차원이라고 가정
a[0.5, 0.5, 0] , b[1, 0, 0]
a x b = |a||b|sin θ = |c|
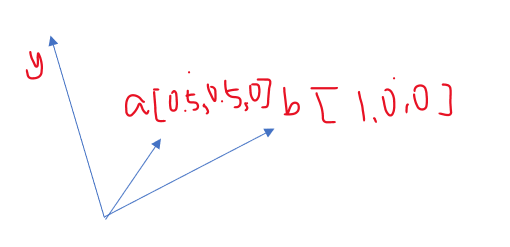
c = [0, 0, ■] = [0, 0, |a||b|sin θ]
행렬연산
[ 1 0 0 ]
[ 0 2 0 ]
[ 0 1 3 ]
^ ^ ^ : 벡터들의 모듬
a b c --->
*내적*
a = [a1, a2, a3, ... , an]
b = [b1, b2, b3 ,... , bn]
a º b = [a1b1 + a2b2 + ... + anbn ]
= 0 + 0 + 0 = 0
즉, a와 b는 직교관계
행렬 = 벡터의 나열
a: 벡터
[a1, a2, ... an]
0 = c1a1 + c2a2 (c1, c2는 스칼라)
ex) a1 = [1,2]
c1 = 3
c1a1 = [3, 6]
c1a1+c2a2를 0으로 만드는 스칼라값 c1,c2가 있을까?
[c1 = 0, c2 = 0] (자명) (trivial)
자명한 해 말고는 해를 찾을 수 없다면 일차 독립이다.
※ 직교하면 일차독립이지만, 일차독립이라고 직교하지 않는다.
※ a º b = 0 <=> a1 ┴ a2 (직교) => a1, a2 일차독립
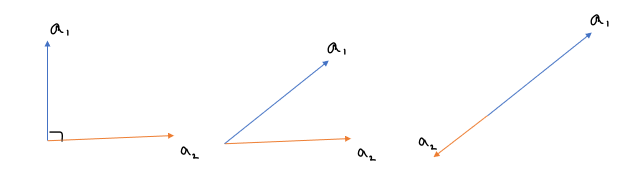
<직교> <일차독립> <일차종속>
직교: 벡터 두 개가 서로를 감시할 수 없음
일차 독립: 벡터 두 개가 서로를 감시할 수 있지만, 감시할 수 없는 영역이 있음.
일차 종속 : 벡터 두 개가 서로의 전부를 감시할 수 있음.
일차독립 a1, a2, ... , an : 벡터, c1, c2, ... , cn : 스칼라
c1a1+ c2a2+ .... + cnan = 0
{c1 ~ cn}의 해가 c1 = ... = cn = 0 이 유일 : 독립
유일하지 않다면 : 종속
[ 1 0 -1 ]
A = [ 1 1 -1 ]
[ 0 1 0 ]
a1 a2 a3
1a1 + 0a2 + 1a3 = 0 -> 즉, 독립 아님
a1과 a3는 종속
일차독립 열벡터 수 = 2 = rank(A)
정복해야할 공간: R^3 = vector space
스칼라를 곱했던 열벡터들: 기저 (basis)
tangentalplane: 구가 있을 때, 구를 접하는 면
basis(기저) : independent (독립)
|_____ > 길이(norm) = 1 (unit basis vector)
rank : 행령상에서 일차 독립인 열벡터의 수
일차독립, 종속, 직교
data encoding
occam's razor
그림(data) -> Encoding layer -> decoding layer-> classify
특징 : 버려지는 차원 있음 > 저차원으로 해석 가능
dim 낮아짐